概念
通过 事前预估 算法 时间开销 T (n) 与 问题规模 n 的关系 (T 表示 time) 函数,来描述该算法的运行时间。
示例 1
// 逐步递增型爱你
public static void main(String[] args) { // n 为问题规模
loveYou(3000);
}
private static void loveYou(int n) {
int i = 1; // ------------------------------------- (1)
while (i <= n) { // ------------------------------- (2)
i++; // --------------------------------------- (3)
System.out.println("I Love You " + i); // ----- (4)
}
System.out.println("I Love You More Than " + n); // (5)
}
结果
I Love You 2995
I Love You 2996
I Love You 2997
I Love You 2998
I Love You 2999
I Love You 3000
I Love You 3001
I Love You More Than 3000
语句 频度 :
(1) 执行 1 次
(2) 执行 3001 次
(3)(4) 执行 3000 次
(5) 执行 1 次
T(3000) = 1 + 3001 + 2 * 3000 + 1
时间开销与问题规模 n 的关系:
T(n) = 3n + 3 ≈ 3n
时间复杂度表达式可以只考虑阶数高的部分
上述表达式可以简化为 T (n) = O (n)
大 O 表示"同阶",同等数量级。即:当 n→∞时,二者之比为常数
计算技巧
(a)加法规则
T(n) = T1(n) + T2(n) = O(f(n)) + O(g(n)) = O(max(f(n), g(n)))
↓—↓—↓—↓
多项相加,只保留最高阶的项,且系数变为 1
(b)乘法规则
T(n) = T1(n) * T2(n) = O(f(n)) * O(g(n)) = O(f(n) * g(n))
↓—↓—↓—↓
多项相乘,都保留
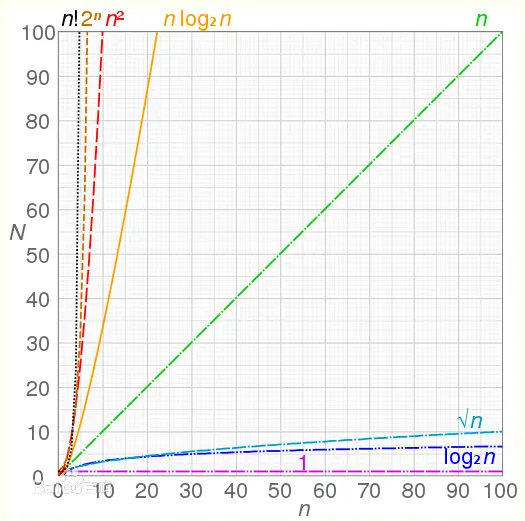
时间复杂度大小关系
示例 2
// 嵌套循环型爱你
public static void loveYou(int n) {
int i = 1;
while (i <= n) {
i++;
System.out.println("I Love You " + i);
for (int j = 1; j <= n; j++) {
System.out.println("I'm Iron Man");
}
}
System.out.println("I Love You More Than " + n);
}
时间开销与问题规模 n 的关系: T(n) = O(n)+O(n2) = O(n2)
示例 3
// 指数递增型爱你
public static void loveYou(int n) {
int i = 1;
while (i <= n) {
i = i * 2; // 每次翻倍
System.out.println("I Love You " + i);
}
System.out.println("I Love You More Than " + n);
}
结果
I Love You 2
I Love You 4
I Love You 8
I Love You 16
I Love You 32
I Love You 64
I Love You 128
I Love You 256
I Love You 512
I Love You 1024
I Love You 2048
I Love You 4096
I Love You More Than 3000
计算上述算法的时间复杂度 T (n):
设最深层循环的语句频度 (总共循环次数) 为 x, 则由循环条件可知,循环结束时刚好满足 2x>n
x = log2n + 1
T(n) = O(x) = O(log2n)+O(1) = O(log2n)
示例 4
// flag 数组中乱序存放了 1~n 这些数
int[] flag = {1...n};
loveYou(flag, 3000);
public static void loveYou(int[] flag, int n) {
System.out.println("I'm Iron Man");
for (int i = 0; i < n; i++) { // 从第一个元素开始查找
if (flag[i] == n) { // 找到元素 n
System.out.println("I Love You " + n);
break; // 跳出循环
}
}
}
计算上述算法的时间复杂度 T (n):
最好 情况: 元素 n 在第一个位置 => T (n) = O (1)
最坏 情况: 元素 n 在最后一个位置 => T (n) = O (n)
平均 情况: 假设元素 n 在任意位置的概率相同为 1 / n => T (n) = O (n)